这一篇会覆盖下面三个版本的 Memory Networks
- Memory Network with strong supervision
- End-to-End Memory Network
- Dynamic Memory Network
涉及下面一些论文:
- Memory Networks (2015)
- End-To-End Memory Networks (2015)
- Ask Me Anything: Dynamic Memory Networks for Natural Language Processing (2016)
- Dynamic Memory Networks for Visual and Textual Question Answering (2016)
首先要明确的是,Memory Networks 只是一种思想或者说一个框架,像一个 base class,里面的各个 module 都可以自己定制。其中基本的一些思路:
- 分层 RNN 的 context RNN
与 context RNN 类似,Memory Network 同样以句子为单位来提取、保存语境信息 - Attention 原理
使用多个 state vector 来保存信息,并从中寻找有用的记忆,而不是寄希望于 final state 存储的信息 - Incorporate reasoning with attention over memory(RAM): Memory Network
使用记忆以及记忆上的 attention 来做推理
Memory Networks (2015)
对应论文:Memory Networks (2015)
Memory Networks 提出的基本动机是我们需要 长期记忆(long-term memory)来保存问答的知识或者聊天的语境信息,而现有的 RNN 在长期记忆中表现并没有那么好。
组件
4 个重要组件:
- I: input feature map
把输入映射为特征向量(input -> feature representation)
通常以句子为单位,一个句子对应一个向量 - G: generalization
使用新的输入数据更新 memories - O: output
给定新的输入和现有的 memory state,在特征空间里产生输出
类比 attention RNN decoder 产生 outputs/logits - R: response
将输出转化为自然语言
流程
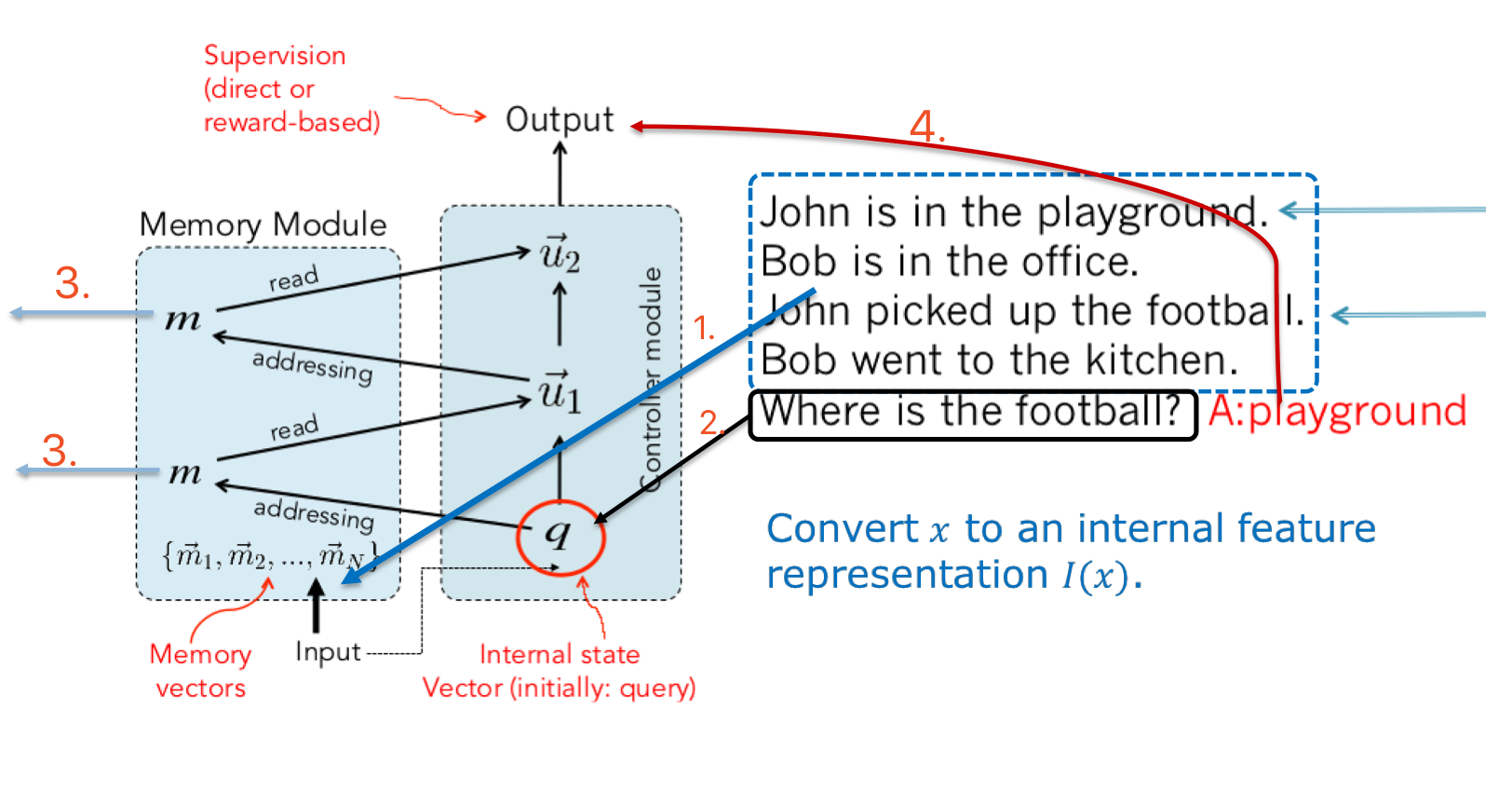
上面的 4 个 component 就对应了整个工作流程:
- 把输入 x 映射为特征向量 I(x)
可以选择多种特征,如 bag of words, RNN encoder states, etc.
如果用 embedding model 来表达文本的话,一个郁闷的地方是 embdding 的参数在不断变化,所以训练时保存的 vector 也要变化……当然这在测试时就成了优势,因为测试时 embedding 参数就固定啦 - 更新 memory mi,$m_i = G(m_i, I(x), m), \forall i.$
将输入句子的特征 x 保存到下一个合适的地址 $m_n$,可以简单的寻找下一个空闲地址,也可以使用新的信息更新之前的记忆
简单的函数如 $m_{H(x)}=I(x)$,H(x) 是一个寻址函数(slot choosing function),G 更新的是 m 的 index,可以直接把新的输入 I(x) 保存到下一个空闲的地址 $m_n$,并不更新原有的 memory,当然更复杂的 G 函数可以去更新更早的 memory 甚至是所有的 memory - 给定新的输入和 memory,计算 output feature o: o=O(I(x),m)
Addressing,寻址,给定 query Q,在 memory 里寻找相关的包含答案的记忆
$qUU^Tm$: 问题 q 和事实 m 的相关程度,当然这里的 q,m 都是特征向量,可以用同一套参数也可以用不同的参数
U:bilinear regression 参数,相关事实的 $qUU^Tm_{true}$ 分数高于不相关事实的分数 $qUU^Tm_{random}$
n 条记忆就有 n 条 bilinear regression score
回答一个问题可能需要寻找多个相关事实,先根据 query 定位到第一条最相关的记忆,再用第一条 fact 和 query 通过加总或拼接等方式得到 u1 然后一起定位第二条
$o_1 = O_1(q,m) = argmax_{i=1,…N} \ s_o(q, m_i)$
$o_2 = O_2(q,m) = argmax_{i=1,…N} \ s_o([q, o_1], m_i)$ - 对 output feature o 进行解码,得到最后的 response: r=R(o)
将 output 转化为自然语言的 response
$r = argmax_{w \in W} \ s_R([q, o_1, o_2], w)$
$s_R(x,y)=xUU^Ty$
可以挑选并返回一个单词比如说 playground
在词汇表上做一个 softmax 然后选最有可能出现的单词做 response,也可以使用 RNNLM 产生一个包含回复信息的句子,不过要求训练数据的答案就是完整的句子,比如说 football is on the playground
Huge Memory 问题
如果 memory 太大怎么办?
- 可以按 entity 或者 topic 来存储 memory,这样 G 就不用在整个 memories 上操作了
- 如果 memory 满了,可以引入 forgetting 机制,替换掉没那么有用的 memory,H 函数可以计算每个 memory 的分数,然后重写
- 还可以对单词进行 hashing,或者对 word embedding 进行聚类,总之是把输入 I(x) 放到一个或多个 bucket 里面,然后只对相同 bucket 里的 memory 计算分数
损失函数
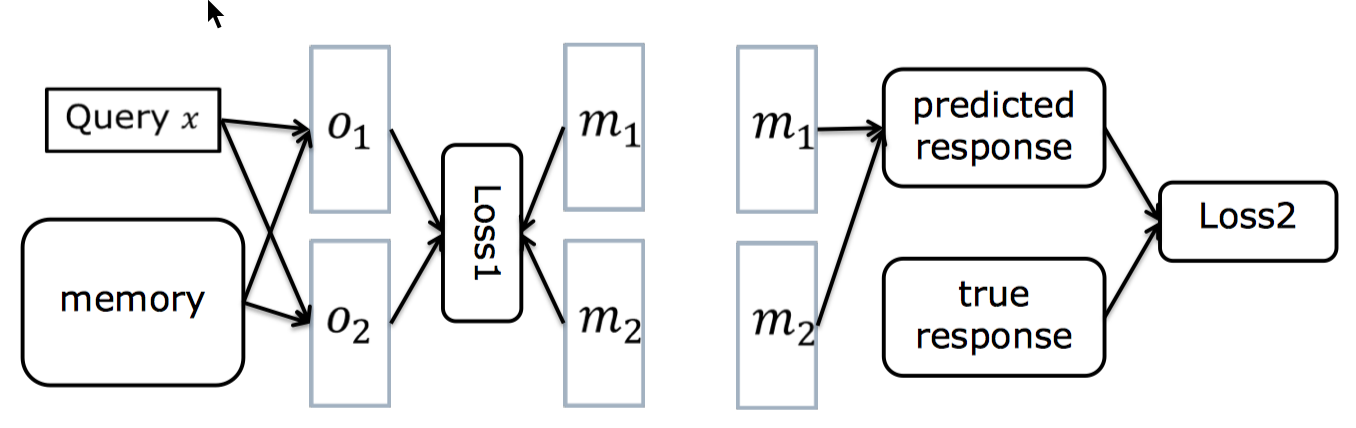
损失函数如下,选定 2 条 supporting fact (k=2),response 是单词的情况: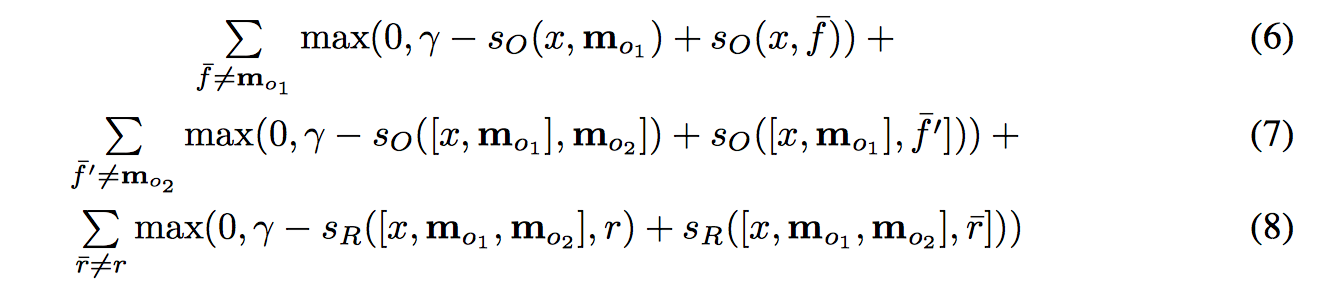
(6) 有没有挑选出正确的第一句话
(7) 正确挑选出了第一句话后能不能正确挑出第二句话
(6)+(7) 合起来就是能不能挑选出正确的语境,用来训练 attention 参数
(8) 把正确的 supporting fact 作为输入,能不能挑选出正确的答案,来训练 response 参数
Performance
在 bAbI QA 部分数据集上的结果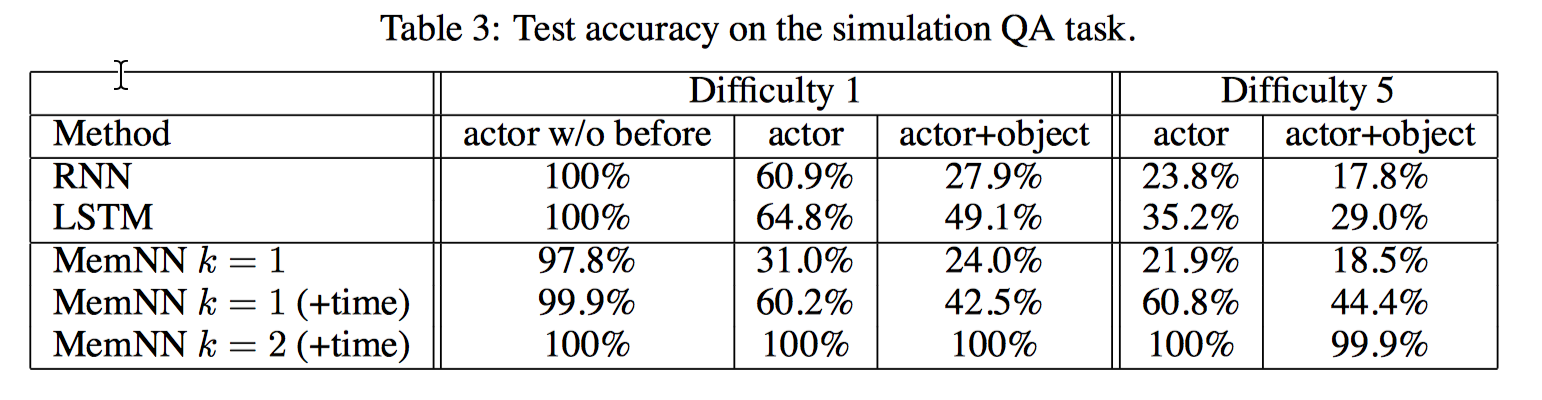
部分 QA 实例:
局限
- 需要很强的标记信息
bAbI 提供了 supporting fact 的 ID,但对大多数 QA 数据而言,并不存在明确的 supporting fact 标记 - Loss2 无法 backpropagate 到模型的左边部分,BP 过程到 m 就停了,并不能 end-to-end 进行训练
这相当于一个链状的贝叶斯网络,考虑 A->B->C 的有向图,B 对应 m,B 不确定的时候,C 依赖于 A,但是当 B 确定的时候,C 就不依赖于 A 了。 也就是说,在给定 m 的情况下,loss2 和前面的参数是独立的,所以优化 loss2 并不能优化左边的参数
End-to-End learning
对应论文:End-To-End Memory Networks (2015)
End-to-End learning 用了 soft attention 来估计每一个 supporting fact 的相关程度,实现了端到端的 BP 过程。
Single Layer
一张图就解决了: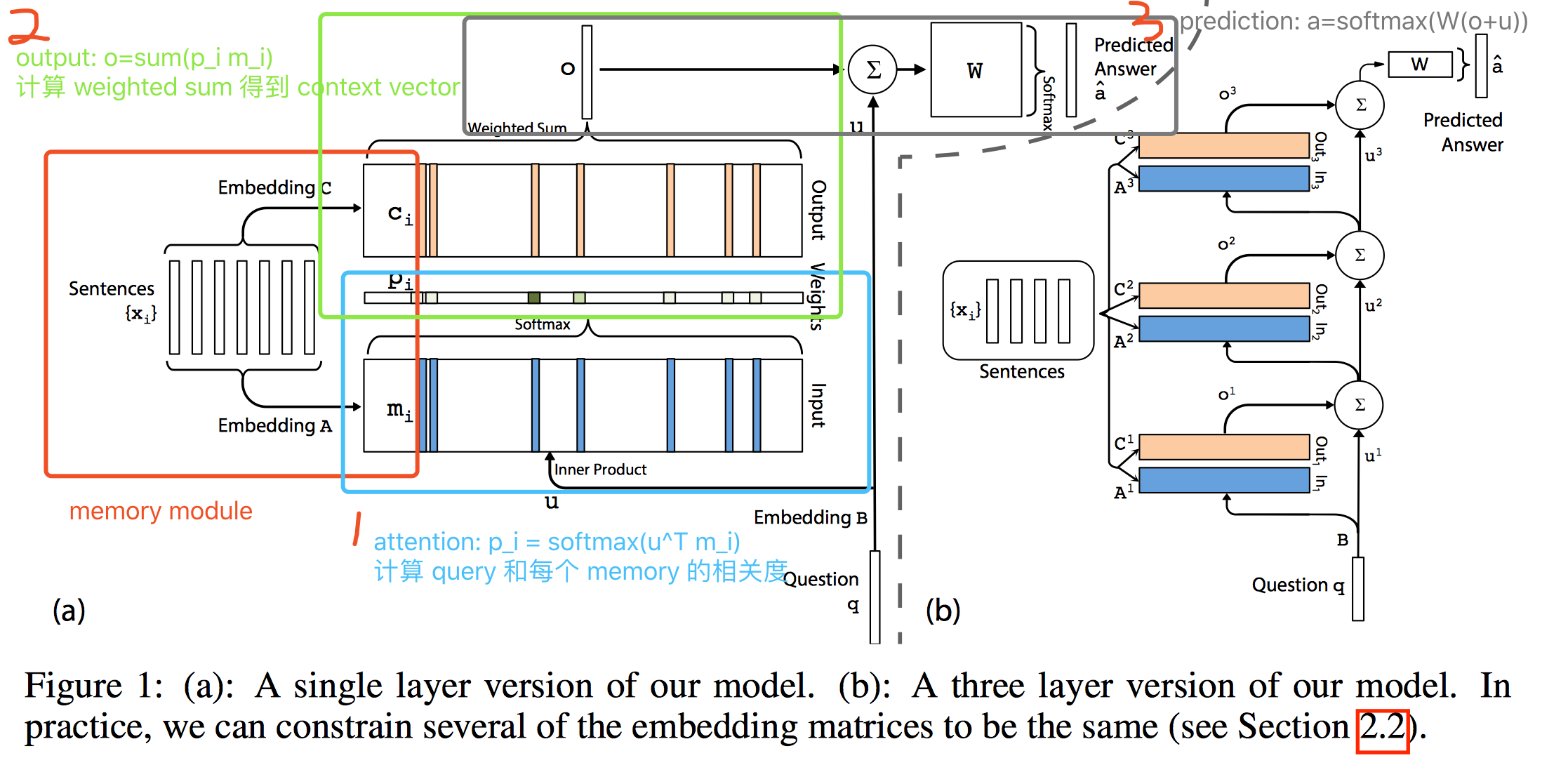
模型输入:
- Input: $x_1, …, x_n$,会被存储到 memory 中
- Query: q
- Answer: a
具体过程(以单层为例):
- 映射到特征空间
{$x_i$} $\xrightarrow{A}$ {$m_i$}
$q \xrightarrow{B} u$ - 计算 attention,得到 query 和 memory 的匹配度,有多少个 memory 就有多少个 $p_i$
$p_i = Softmax(u^Tm_i)$ - 得到 context vector
$o = \sum_ip_ic_i$
和 Memory Networks with Strong Supervision 版本不同,这里的 output 是加权平均而不是一个 argmax - context vector 和 query 一起,预测最后答案,通常是一个单词
$\hat a=Softmax(W(o+u))$ - 对 $\hat a$ 进行解码,得到自然语言的 response
$\hat a \xrightarrow{C} a$
其中,
A: intput embedding matrix
C: output embedding matrix
W: answer prediction matrix
B: question embedding matrix
损失函数是交叉熵,用 SGD 训练。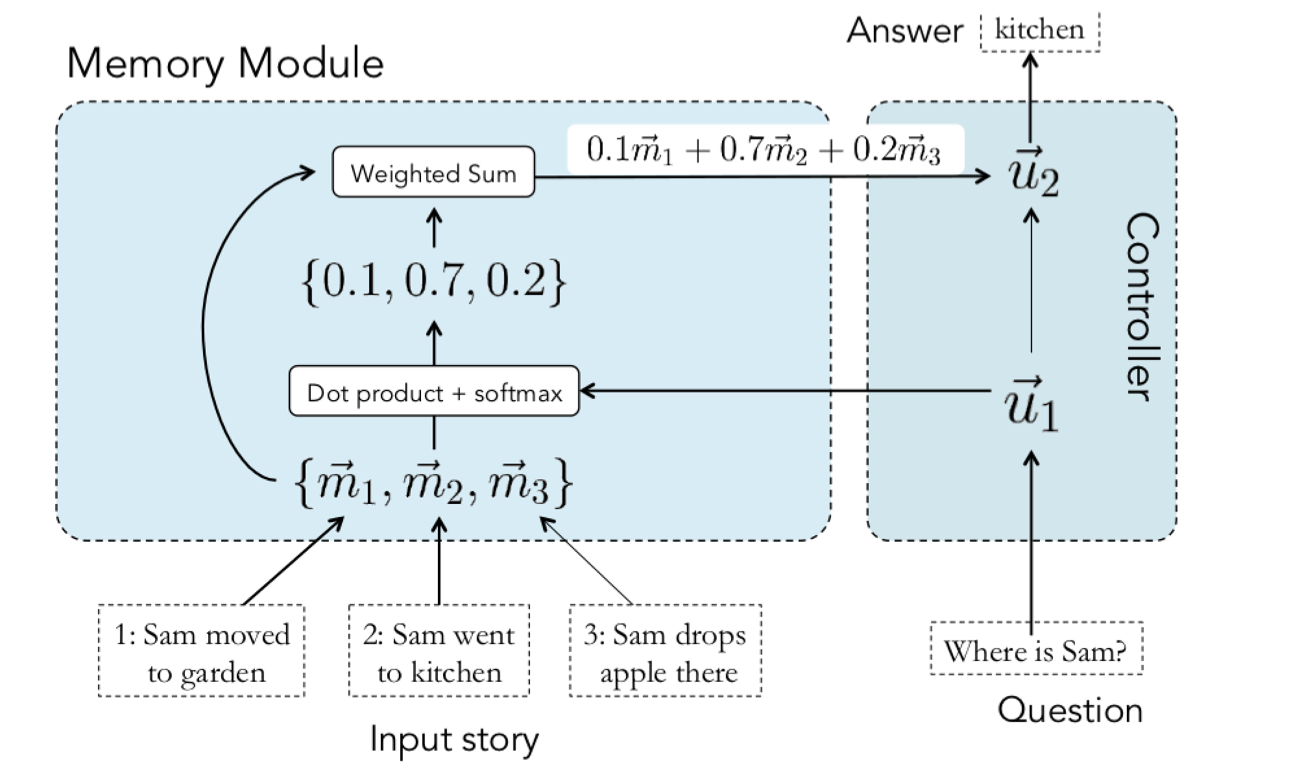
Multi-hop Architecture
多层结构(K hops)也很简单,相当于做多次 addressing/多次 attention,每次 focus 在不同的 memory 上,不过在第 k+1 次 attention 时 query 的表示需要把之前的 context vector 和 query 拼起来,其他过程几乎不变。
$u^{k+1}=u^k + o^k$
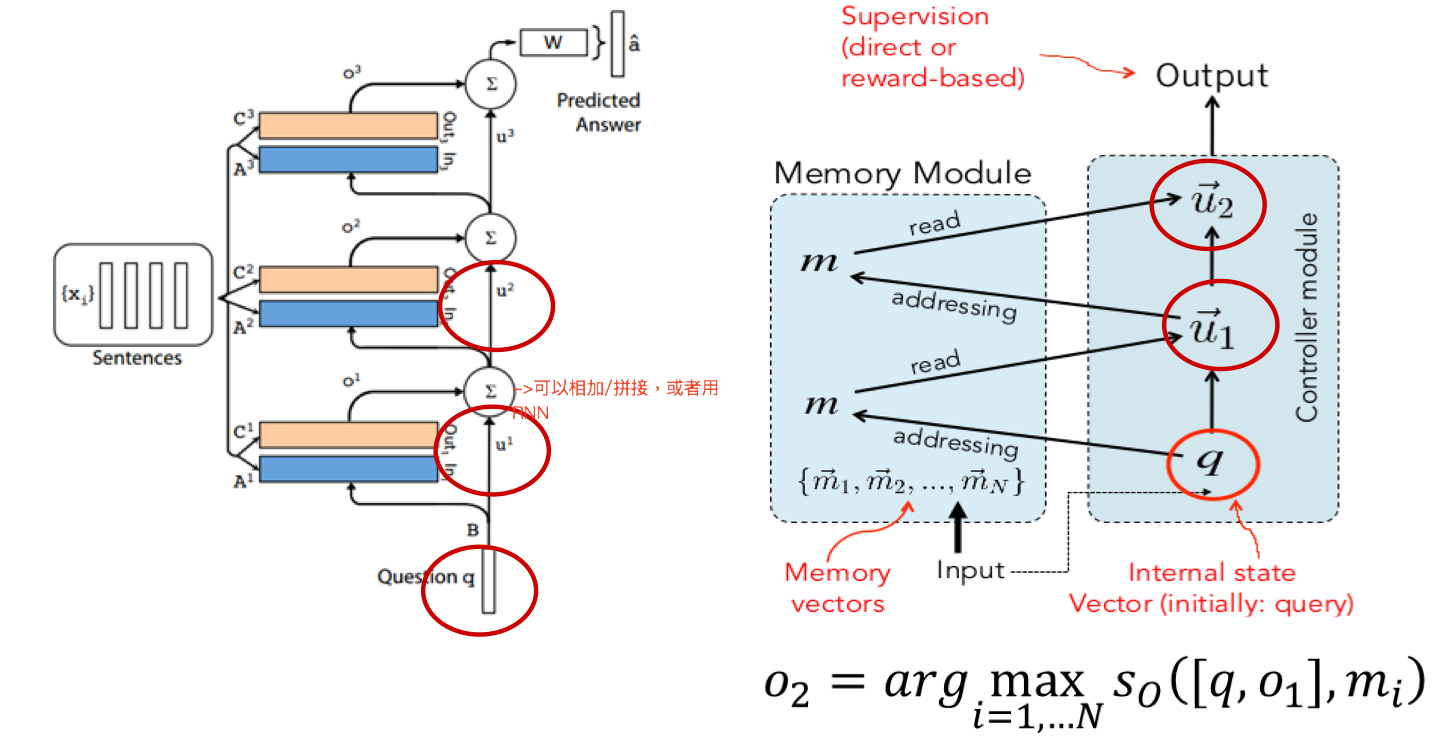
一些技术细节
通常来说 encoding 和 decoding 的词向量参数是不一样的,因为一个是单词-词向量,一个是 隐状态-词向量。
- Adjacent
前一层的输出是这一层的输入
$A^{k+1}=C^k$
$W^T=C^L$
$B=A^1$ - Layer-wise(RNN-like)
不同层之间用同样的 embedding
$A^1=A^2=…=A^K$
$C^1=C^2=…=C^K$
可以在 hop 之间加一层线性变换 H 来更新 $\mu$
$u^{k+1}=Hu^k+o^k$
Dynamic Memory Networks
对应论文:Ask Me Anything: Dynamic Memory Networks for Natural Language Processing (2016)
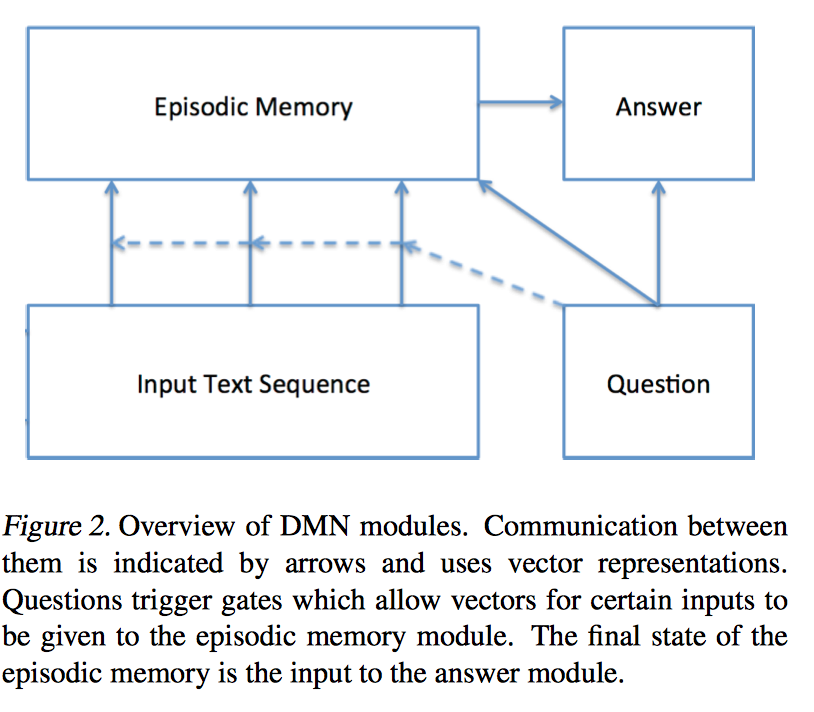
Input Module
这一部分像是一个 semantic memory。输入可以是一个/多个句子,一篇/几篇文章,包含语境信息和知识库等,使用 RNN 进行 encoding,每一个句子编码成固定维度的 state vector。
具体做法是把句子拼到一起(每个句子结尾加标记符 EOS),用 GRU-RNN 进行编码,如果是单个句子,就输出每个词的 hidden state;如果是多个句子,就输出每个句子 EOS 标记对应的 hidden state,其实相当于分层 RNN 的下面一层。
$$h_t=GRU(L[w_t], h_{t-1})$$
$L[w_t] $ 是 word embedding。
Question Module
输入是 question 对应的词序列,同样用 GRU-RNN 进行编码。
$$q_t=GRU([L[w_t^Q], q_{t-1})$$
同样的,L 是词向量参数,和 input module 的 L 相同。输出是 final hidden state
Episodic Memory Module
由 internal memory, attention mechansim, memory update mechanism 组成。 输入是 input module 和 question module 的输出。
把 input module 中每个句子的表达(fact representation c)放到 episodic memory module 里做推理,使用 attention 原理从 input module 中提取相关信息,同样有 multi-hop architecture。
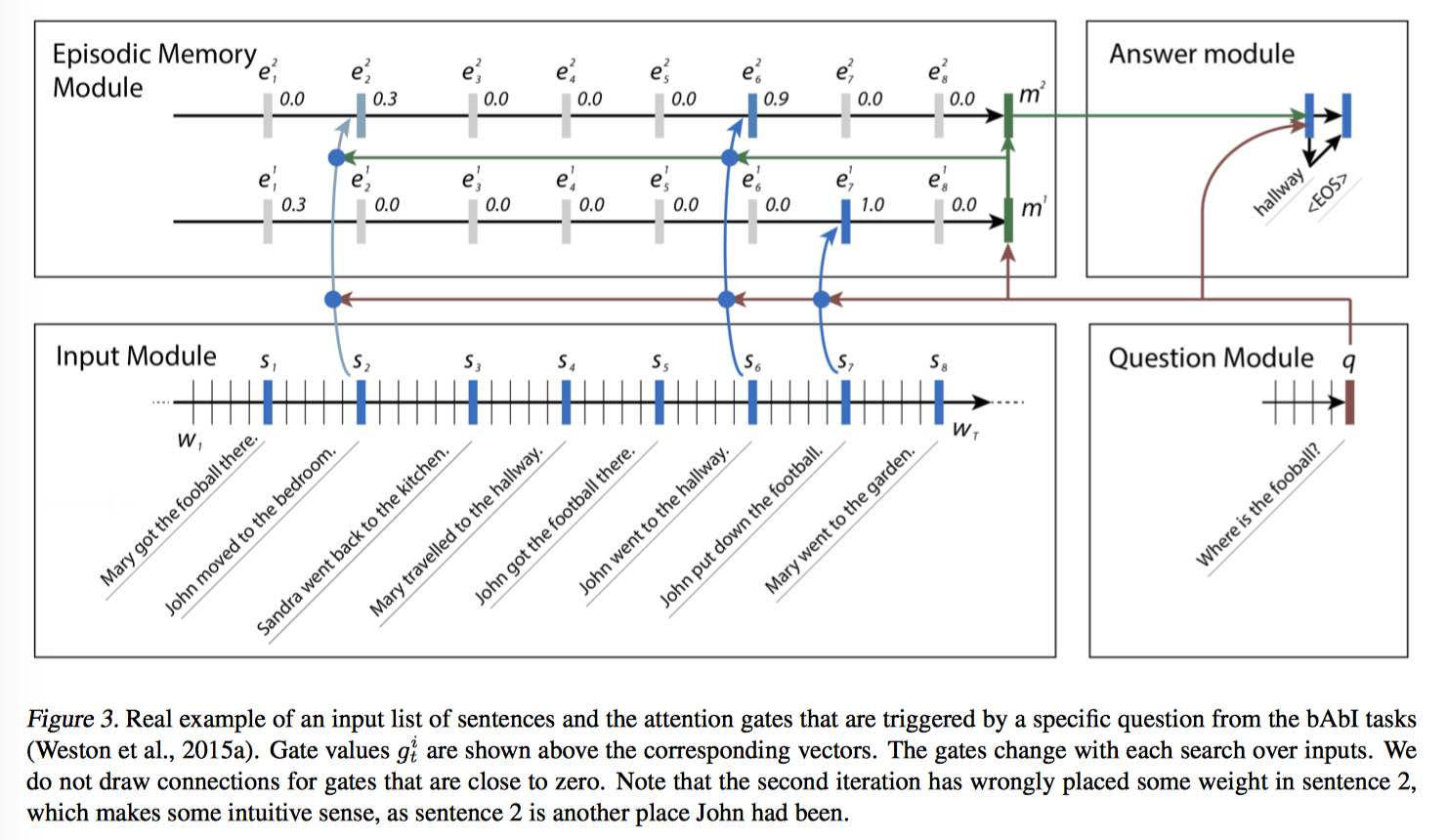
Attention Mechanism
觉得论文里的 attention mechanism 和 memory update mechanism 描述的有点问题,个人以为 attention mechanism 的目的还是生成 context vector,memory update mechanism 的目的是更新 memory,所以把部分公式按自己的理解移动了下,便于理解。
计算 query 和 fact 的分数,query 和上一个 memory $m^{i-1}$ 作为输入产生输出 episode $e^i$。要注意的是,End-to-End MemNN 的 attention 用的是 linear regression,DMN 用的是 gating function,一个两层的前向神经网络。
在每一轮迭代中,都有输入:
- $c_t$(input module 中第 t 个位置的 fact vector)
- 上一轮迭代得到的 memory $m_{i-1}$
- question q
利用 gating function 计算第 t 个位置的得分 $g^i_t=G(c_t, m_{i-1}, q)$。G 是一个两层的前向神经网络的 score function,不过描述 input, memory, question 相似度的 feature vector z(c,m,p) 是人工定义的,这也成为了之后 DMN+ 的一个优化点。
计算完每一次迭代每一个位置的分数后,来更新 episode $e^i$,或者说产生 context vector。输入是 $c_1, …, c_{T_C}$,和它们的 gate score $g^i_t$。
$$ h^i_t=g^i_tGRU(c_t, h^i_{t-1})+(1-g^i_t)h^i_{t-1}$$
$$e^i=h^i_{T_C}$$
总结一下,这部分 attention mechanism 的目的是生成 episode $e^i$,$e^i$ 是第 t 轮迭代的所有相关 input 信息的 summary。与 End-to-End MemNN 不同的是,End-to-End 用了 soft attention,也就是加权和来计算 context,而这里用了 GRU。
Memory Update Mechanism
上一步算的 episode $e^i$ 以及上一轮迭代的 memory $m^{i-1}$ 作为输入 来更新 episodic memory $m^i$。
$$m^i=GRU(e^i, m^{i-1})$$
输出是最后一次迭代的 $m=m^{T_M}$
End-to-End MemNN 的 memory update 过程里,第 k+1 次 query vector 直接是上一个 context vector 和 query 的拼接,$u^{k+1}=u^k + o^k$。而 DMN 里,采用了 RNN 做非线性映射,用 episode $e^i$ 和上一个 memory $m^{i-1}$ 来更新 episodic memory,其 GRU 的初始状态包含了 question 信息,$m^0=q$。
Episodic Memory Module 需要一个停止迭代的信号。一般可以在输入中加入一个特殊的 end-of-passes 的信号,如果 gate 选中了该特殊信号,就停止迭代。对于没有显性监督的数据集,可以设一个迭代的最大值。
总结一下,这部分 memory update mechanism 的目的是生成 t 时刻的 episode memory $m^t$,最后一个 pass 的$m^T$ 将包含用于回答问题 q 的所有信息。
Example Understanding
来用例子解释下 Episodic Memory Module 上面那张图,question 是 where is the football? 第一次迭代找到的是第 7 个句子,John put down the football,第二次找到第 6 个句子 John went to the hallway,第三次找到第 2 个句子 John moved to the bedroom。
多次迭代第一次找到的是字面上最相关的 context,然后一步步迭代会逐渐定位到真正语义相关的 context,这感觉上就是一个推理的过程。
Answer Module
使用了 GRU-RNN 作为 decoder。输入是 question module 的输出 q 和上一时刻的 hidden state $a_{t-1}$,初始状态是episode memory module 的输出 $a_0=m^{T_M}$
$$
\begin{aligned}
y_t=Softmax(W^{(a)}a_t) \\
a_t=GRU([y_{t-1}, q], a_{t-1}) \\
\end{aligned}
$$
训练
使用 cross-entroy 作为目标函数。如果数据集有 gate 的监督数据,还可以将 gate 的 cross-entroy 加到总的 cost上去,一起训练。训练直接使用 backpropagation 和 gradient descent 就可以。
小结
总的来说,DMN 在 addressing,memory 提取,query/memory update 部分都用了 DL 手段,相比于 End-to-End MemNN 更为复杂。
DMN+
对应论文:Dynamic Memory Networks for Visual and Textual Question Answering (2016)
DMN 存在的两个问题:
- 输入模块只考虑了过去信息,没考虑到将来信息
- 只用 word level 的 GRU,很难记忆远距离 supporting sentences 之间的信息
这一部分重点讲与 DMN 不同的地方。
Input Module
DMN+ 把 single GRU 替换成了类似 hierarchical RNN 结构,一个 sentence reader 得到每个句子的 embedding,一个 input infusion layer 把每个句子的 embedding 放入另一个 GRU 中,得到 context 信息,来解决句子远距离依赖的问题。HRED 相关思路见 论文笔记 - HRED 与 VHRED。这里还做了一些微调,sentence reader 用的是 positional encoding,input fusion layer 用了双向 GRU,兼顾了过去和未来的信息。
用 positional encoding 的原因是在这里用 GRU/LSTM 编码句子计算量大而且容易过拟合(毕竟 bAbI 的单词量很小就几十个单词。。),这种方法反而更好。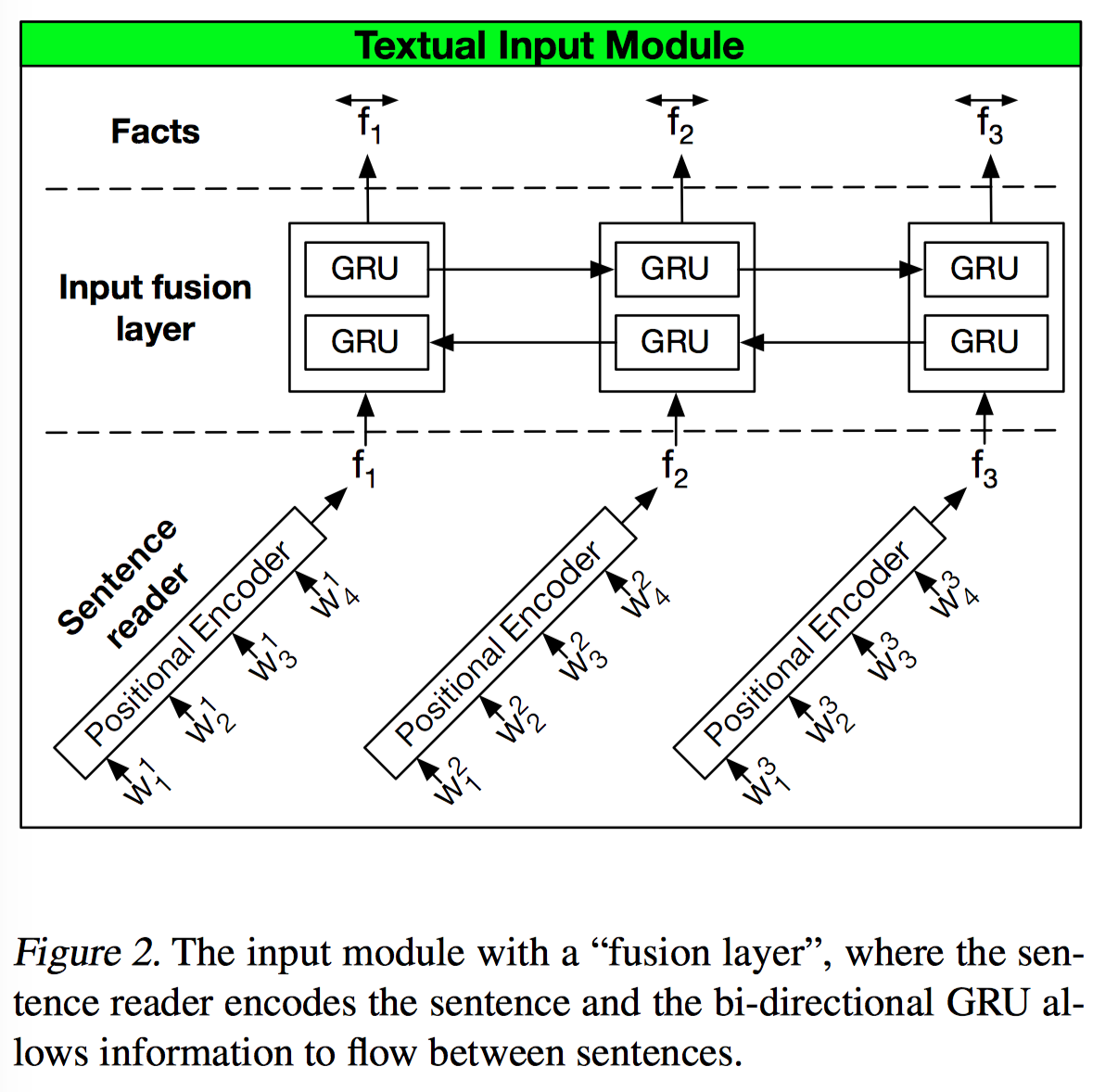
除了处理文本信息,作者也提出了图像信息的方案,CNN+RNN,把局部位置的图像信息当做 sentence 处理,在这不多介绍。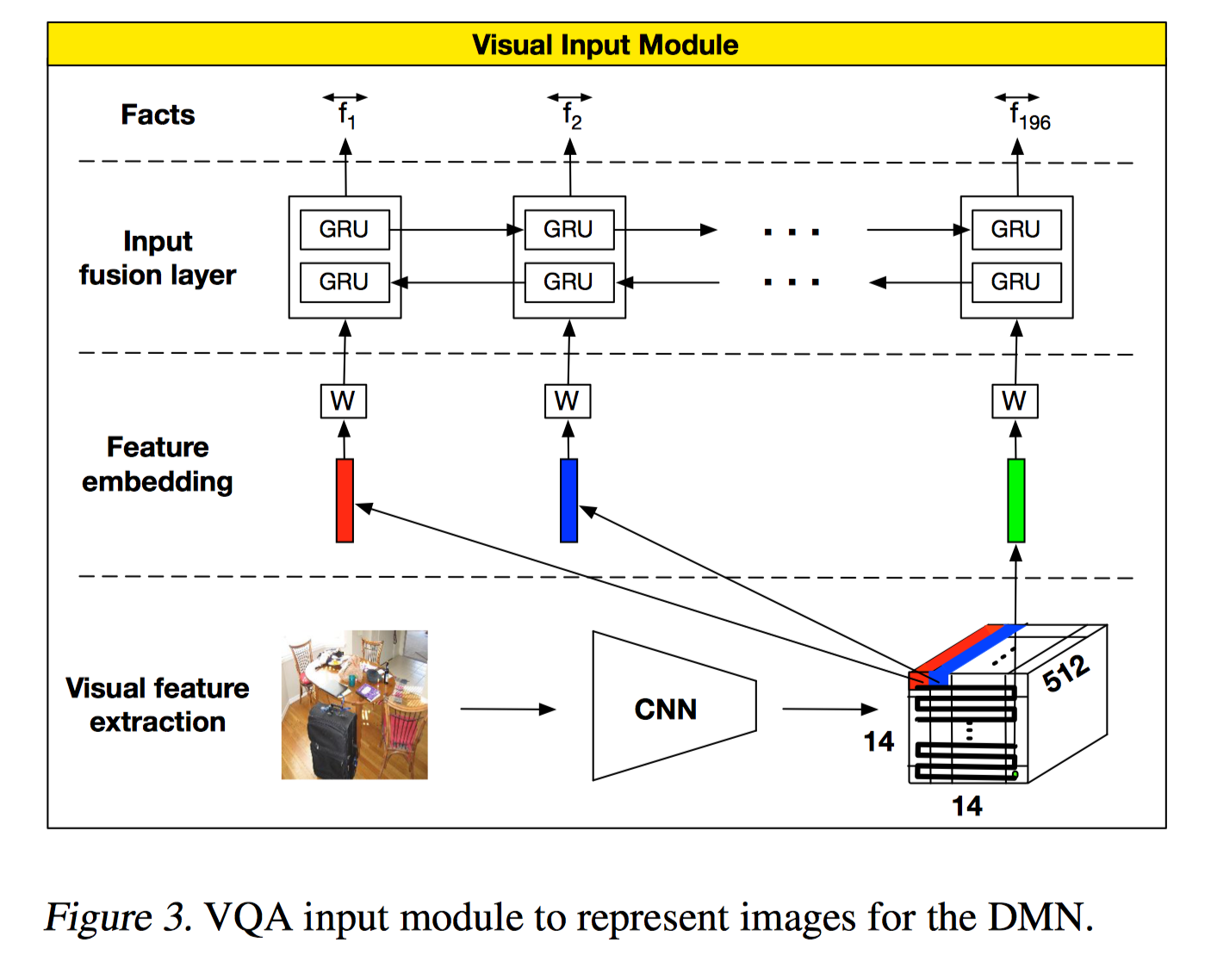
Episodic Memory Module
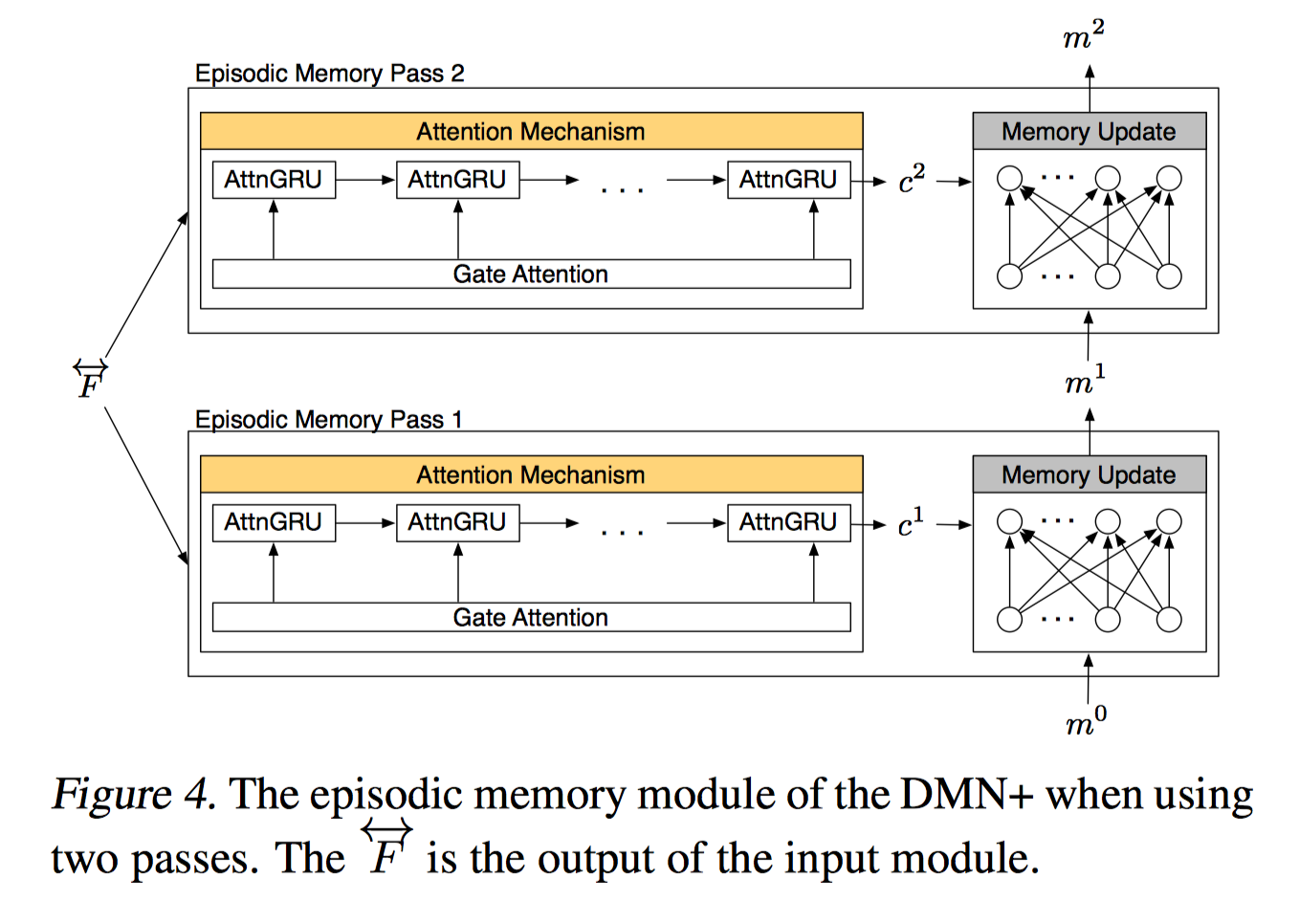
Attention Mechanism
仍然是人工构造特征向量来计算 attention,但与之前版本的 DMN 相比更为简化,省去了两项含有参数的部分,减少了计算量。另外与 DMN 不同的是,gate 值不是简单的二层前馈网络的结果,而是接着计算了一个 sofmax 评分向量。
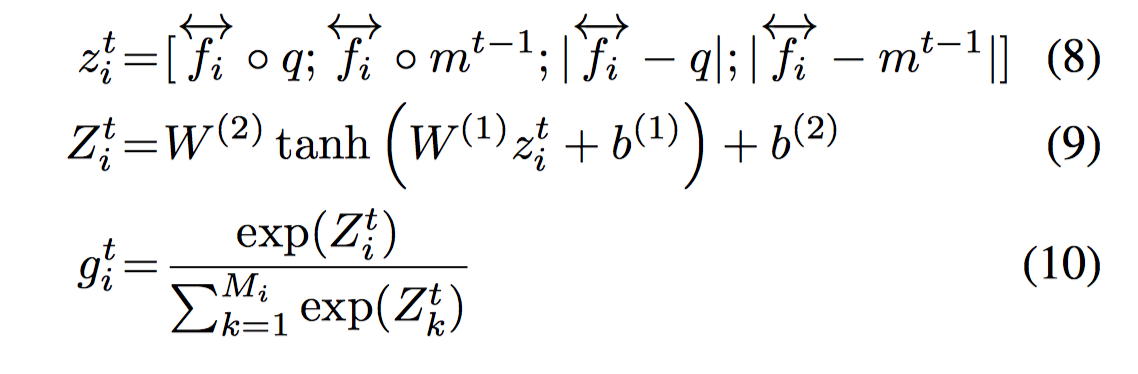
也就是说,从公式上看,相对于 DMN,式 8 更为简洁,式 9 不变(结果就是 DMN 的 gate 值),增加了式 10。
进行到下一步关于 context vector 的计算,两种方案,一种是 soft attention,简单的加权求和,另一种是 attention based GRU。
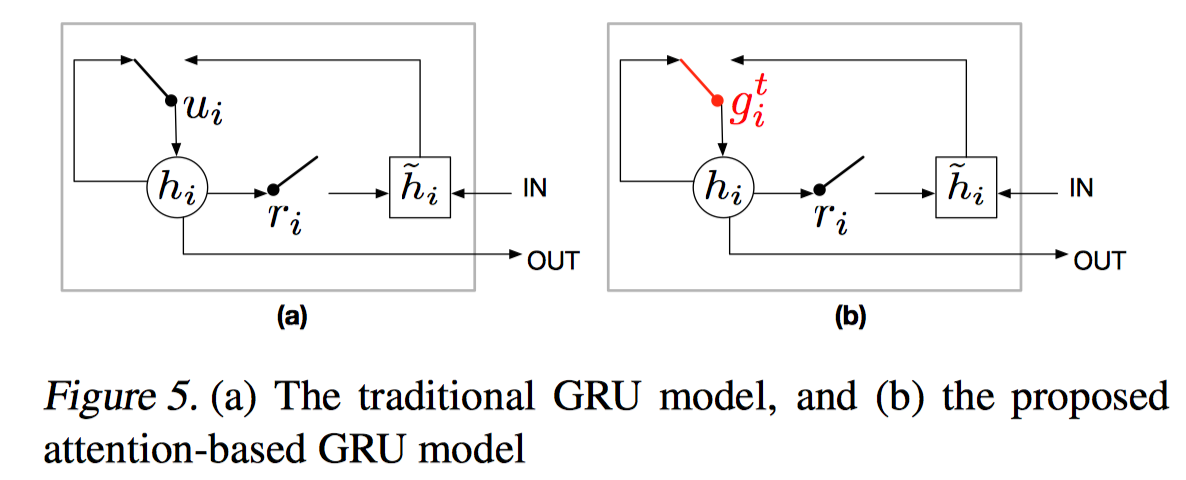
AttnGRU 考虑了输入 facts 的位置和顺序信息(position and ordering),或者说是时序信息。在得到 attenion 后,把 attention 作为 gate,如上图,把传统 GRU 中的 update gate $u_i$ 替换成了 attention 的输出 $g^t_i$,这样 gate 就包含了 question 和前一个 episode memory 的知识,更好的决定了把多少 state 信息传递给下一个 RNN cell。同时这也大大简化了 DMN 版本的 context 计算。
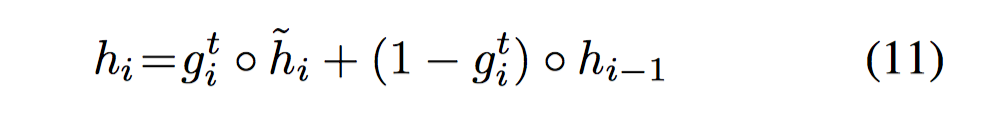
$\hat h$ 是更新的 state,$h_{i-1}$ 是传入的上一时刻的 state,$g^t_i$ 是 attention value,是一个由 softmax 产生的标量(scalar)而不是 sigmoid 激活产生的 vector $u_i \in R^{n_H}$,context vector 是 GRU 的 final hidden state。
AttnGRU 要优于 weighted sum,因为使用了一些时间上的关系,比如小明在操场,小明回了家,小明进了卧室,这些事实实际上有先后关系,而 weighted sum 不一定能反映这种时序关系。
Memory Update Mechanism
DMN 中 memory 更新采用以 q 向量为初始隐层状态的 GRU 进行更新,用同一套权重,这里替换成了一层 ReLU 层,实际上简化了模型。
$$m^t = ReLU(W^t[m^{t-1};c^t;q]+b)$$
其中 ; 表示拼接,这能进一步提高近 0.5% 的准确率。
Performance
最后上一个不同模型的 performance 比较图。